Rata równa i rata malejąca w kredycie hipotecznym. Jak wyliczyć?

Opublikowano: 28 Lip 2022 Agnieszka Kłak 11 min. czytania

Kategoria: Poradnik Hipoteczny

Rata stała a rata malejąca – podstawowa charakterystyka

Pierwszą podstawową różnicą pomiędzy omawianymi rodzajami rat będzie wielkość każdej z nich w czasie. Wielkość raty stałej pozostanie niezmienna na przestrzeni trwania naszego kredytu. Przynajmniej w założeniu, ponieważ jeżeli oprocentowanie kredytu hipotecznego jest zmienne, to oczywiście rata może ulec zmianie na skutek zmiany stóp procentowanych (więcej o tym przeczytasz tutaj).

Niemniej jednak, w harmonogramie, który zostanie załączony do naszej umowy kredytowej będzie widniała taka sama rata w każdym miesiącu. Rata malejąca natomiast, będzie zgodnie z harmonogramem maleć w czasie. Bank wyliczy ją w taki sposób, aby na początku była większa, a z każdą zapłaconą ratą się zmniejszała.

Wysokość raty równej w harmonogramie jest zawsze taka sama. Rata malejąca maleje w czasie.

W racie równiej odsetki maleją, a kapitał spłacany rośnie z każdą ratą.
W racie malejącej kapitał spłacany jest zawsze taki sam, a odsetki maleją.

Z czego składa się każda rata?

Każda rata, niezależnie do rodzaju, będzie składała się z dwóch części: kapitałowej i odsetkowej. Z każdą ratą pomniejszam saldo zadłużenia w stosunku do banku (czym jest saldo zadłużenia przeczytasz tutaj) oraz płacę odsetki od aktualnego salda. Bank musi zatem wyliczyć ratę tak, abym w okresie trwania kredytu spłacił cały kapitał, który pożyczyłem w banku oraz oddał odsetki, które płaciłem od wykorzystywanego kapitału.

I tu dochodzimy do kolejnej różnicy w racie malejącej i racie stałej. Tą różnicą będzie inna proporcja spłacanego kapitału i odsetek zawartych w racie. Rata malejąca charakteryzuje się tym, że część kapitałowa raty zawsze będzie stała. Zmieniać się będzie natomiast część odsetkowa – wypłynie ona na spłatę kredytu tak, że cała rata będzie niższa (zakładając oczywiście, że nie jesteśmy w okresie karencji i cały czas spłacamy kapitał). Natomiast w racie równiej część kapitałowa będzie rosnąć z każdą ratą, a część odsetkowa będzie maleć.

Dlaczego proporcje spłacanego kapitału i odsetek będą się zmieniać?

Odpowiedzi na powyższe pytanie należy poszukać w sposobie obliczenia raty. Zobaczmy jak możemy obliczyć wysokość raty kredytu hipotecznego na przykładzie.

Określmy sobie parametry przykładu: Klient bierze kredyt hipoteczny. Wartość kwoty kredytu to 360 000 PLN na okres 30 lat (360 miesięcy). Kredyt jest oprocentowany 4% w skali roku. Zacznijmy od obliczenia raty malejącej ponieważ wysokość tej można policzyć na kalkulatorze.

Stwierdziliśmy powyżej, że w przypadku raty malejącej część kapitałowa będzie zawsze równa. Aby obliczyć jej wysokość wystarczy podzielić kwotę kredytu przez liczbę miesięcy:

360 000 PLN / 360 miesięcy = 1000 PLN

Ile natomiast będą wynosić odsetki w pierwszym miesiącu? Musimy pomnożyć saldo zadłużenia razy oprocentowanie roczne i podzielić przez ilość miesięcy w roku. Równanie będzie wyglądało następująco:

360 000 x 4% / 12 = 1200 PLN

Łącznie nasza rata w pierwszym miesiącu będzie wynosiła 1000 + 1200 = 2200 PLN. Jak obliczyć ratę w drugim miesiącu? Rata kapitałowa przez cały okres kredytu się nie zmieni – będzie wynosić 1000 PLN. Rata odsetkowa zmaleje, ponieważ zmniejszyło się saldo zadłużenia. O ile? Po pierwszym miesiącu o spłacony kapitał, czyli 1000 PLN. Policzmy zatem odsetki w drugim miesiącu :

359 000 x 4% / 12 = 1196,67 PLN

Łączna rata w drugim miesiącu będzie wynosić 2196,67 PLN. I tak z każdym miesiącem – łączna wysokość raty będzie maleć ponieważ zmniejszać się będzie saldo zadłużenia o spłacany kapitał, a co za tym idzie Klient będzie płacił mniejsze odsetki. W ostatnim miesiącu kredytu saldo zadłużenia będzie wynosić 1000 PLN. Klient zatem zapłaci ratę w wysokości:

1000 PLN (kapitał) + (1000 *4% / 12) (odsetki) = 1000 + 3,33 = 1003,33 PLN

A jak liczymy raty stałe?

I tu niestety pojawia się trudność. Skoro będziemy płacić tyle samo w całym okresie kredytowania to bardzo dokładnie trzeba obliczyć ratę kredytu, aby Klient spłacił i kapitał i odsetki. A przecież spłacany kapitał będzie zmniejszał saldo, więc odsetki będą malały. A skoro rata jest równa i odsetki będą malały to kapitał spłacany z każdą ratą będzie rósł. Co zatem zrobić, aby wyliczyć ratę równą?

Możemy sięgnąć do jednego z kalkulatorów w Internecie, które mają zaszyty odpowiedni algorytm liczenia lub wyprowadzić samodzielnie odpowiednią funkcję w Excelu. Aby mieć satysfakcję z przygotowanego samodzielnie kalkulatora spójrzmy, jak policzyć ratę stałą w Excelu. W pierwszej kolejności w osobne komórki wprowadzamy dane: roczna stopa procentowa, liczba miesięcznych rat, kwota kredytu. Następnie w nową komórkę wpisujemy wzór:

=-PMT(stopa procentowa/12;liczba miesięcznych rat;kwota kredytu)

Klikamy enter i Excel policzy nam ratę. Podstawmy zatem do wzoru:

=-PMT(4%/12;360;360000)

Wysokość raty stałej będzie wynosiła 1718,70 PLN.

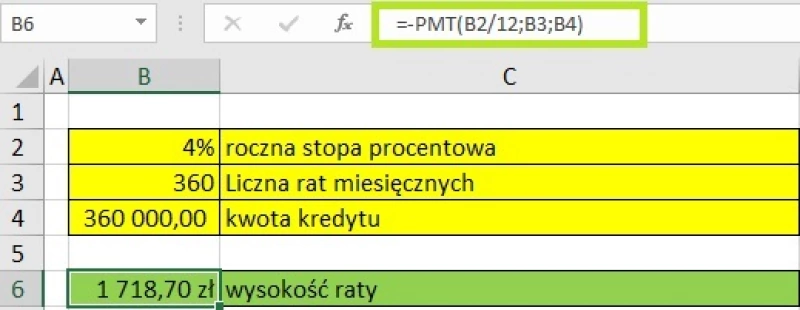
 Rys.1 Sposób wyliczania raty równej w excelu

Wiemy już, jak obliczyć wysokość raty. Potwierdźmy jeszcze tezę, że kapitał rośnie, a odsetki maleją. W jaki sposób? Ile odsetek zapłaci Klient w pierwszej racie? Saldo zadłużenia * oprocentowanie / 12 – 360 000 PLN * 4% / 12 = 1200 PLN. Skoro odsetki wynoszą 1200 PLN, a cała rata 1718,70 PLN to Klient w pierwszej racie spłaci 518,70 PLN kapitału. Podstawą do obliczenia odsetek drugiej raty będzie oczywiście saldo w drugim miesiącu. To wynosi 360 000 minus 518,70, czyli 359 481,30 PLN. Odsetki w drugim miesiącu będą wynosić: 359 481,3 * 4% /12 = 1198,27 PLN. W drugim miesiącu spłacimy zatem następujący kapitał: 1718,70 minus 1198,27 = 520,43 PLN. Odsetki maleją, spłacany kapitał rośnie.

Co bardziej się opłaca?

Wiemy już, jak policzyć wysokość każdego rodzaju raty. Pytanie zatem, jaki harmonogram spłaty będzie tańszy dla Klienta? Odpowiedź jest prosta i logiczna – w racie malejącej od początku spłacamy więcej kapitału w związku z czym przez cały okres trwania kredytu zapłacimy mniej odsetek. Rata malejąca będzie dla Klienta tańsza. Pytanie tylko, o ile? I tu znów musimy sięgnąć do obliczeń. Aby obliczyć ile zapłacimy odsetek w kredycie z ratą stałą wystarczy zsumować łączną kwotę zapłaconych rat w okresie trwania kredytu i odjąć od tej kwoty pożyczony kapitał: (1718,70 *360) – 360 000 = 618 732 – 360 000 = 258 732 PLN. W kredycie z ratą stałą w całym okresie zapłacimy zatem 258 732 PLN odsetek. W kredycie z ratą malejącą dla porównania zapłacimy 216 600 PLN odsetek. Kredyt z ratą mającą będzie tańszy o 42 132 PLN.

Jaką spłatę wybrać?

Udowodniliśmy na liczbach, że kredyt z ratą malejącą będzie tańszy dla Klienta. Oczywistym zatem wyborem powinien być właśnie ten rodzaj spłaty. Niestety, wybór nie jest tak prosty. Wszystko zależy bowiem od zasobności naszego portfela, a co za tym idzie zdolności kredytowej. Nie zawsze będzie nas stać na to, aby płacić wyższą ratę. Bank licząc naszą zdolność kredytową też policzy ją do pierwszej, najwyższej raty. Może się zatem okazać, że dla raty równej dostaniemy pozytywną decyzję kredytową, a dla raty malejącej negatywną – bank oceni, że nie stać nas na płacenie wyższego zobowiązania. Ostateczny wybór zależy od tego, czy będzie nas stać na płacenie wyższej raty oraz od naszych indywidualnych preferencji co do harmonogramu spłaty.

Obecnie rynek kredytów dysponuje wieloma narzędziami do wsparcia klienta w procesie wyboru produktu odpowiedniego dla jego potrzeb. Jedynym z takich narzędzi jest m.in. porównywarka rat kredytu, która pozwala nam oszacować wartości raty z podziałem na ratę stałą i ratę malejącą. Wnioskując o przygotowanie symulacji warto zawsze zwrócić się do swojego doradcy o przygotowanie dwóch rodzajów symulacji. Choć kredyt z ratą malejącą to wyższa rata w pierwszych latach kredytowania może okazać się, że suma kosztów odsetkowych będzie mniejsza niż w przypadku kredytu z ratą stałą. Warto o to zapytać swojego doradcę kredytowego.

Tagi: kapitałrata malejącarata odsetkowarata annuitetowaratakredyt hipoteczny

Dodano: 01.08.2019